Unidad 2 Control estadístico de calidad.

Estadística Descriptiva.

 Rama de la Estadística Matemática que trata los métodos para organizar la información numérica para su mejor interpretación.

La estadística descriptiva implica la abstracción de varias propiedades del conjunto de observaciones, mediante el empleo de métodos gráficos, tabulares o numéricos. Entre estas propiedades están la frecuencia con que se dan varios valores en la observación, la noción de un valor típico o usual, la cantidad de variabilidad en un conjunto de datos observados y la medida de relaciones entre 2 o más variables.

El campo de la estadística descriptiva no tiene que ver con las implicaciones o conclusiones que se puedan deducir del conjunto de datos. La estadística descriptiva sirve como método para organizar datos y poner de manifiesto sus características esenciales con el propósito de llegar a conclusiones.

Estadística Inferencial

Se refiere al proceso de lograr generalizaciones acerca de las propiedades del todo, población, partiendo de lo específico, muestra. Las cuales llevan implícitos una serie de riesgos. Para que éstas generalizaciones sean válidas la muestra deben ser representativa de la población y la calidad de la información debe ser controlada, además puesto que las conclusiones así extraídas están sujetas a errores, se tendrá que especificar el riesgo o probabilidad que con que se pueden cometer esos errores. La estadística inferencial es el conjunto de técnicas que se utiliza para obtener conclusiones que sobrepasan los límites del conocimiento aportado por los datos, busca obtener información de un colectivo mediante un metódico procedimiento del manejo de datos de la muestra.

En sus particularidades la Inferencia distingue la Estimación y la Contrastación de Hipótesis. Es estimación cuando se usan las características de la muestra para hacer inferencias sobre las características de la población. Es contrastación de hipótesis cuando se usa la información de la muestra para responder a interrogantes sobre la población.

7 Herramientas básicas de la calidad

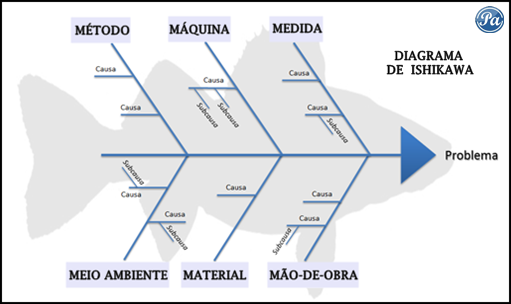
1.   Diagrama de ishikawa: 

También llamado diagrama de causa-efecto o diagrama causal, se trata de un diagrama que por su estructura ha venido a llamarse también: diagrama de espina de pez, que consiste en una representación gráfica sencilla en la que puede verse de manera relacional una especie de espina central, que es una línea en el plano horizontal, representando el problema a analizar, que se escribe a su derecha. Es una de las diversas herramientas surgidas a lo largo del siglo XX en ámbitos de la industria y posteriormente en el de los servicios, para facilitar el análisis de problemas y sus soluciones en esferas como lo son; calidad de los procesos, los productos y servicios.

 

2.   Hoja de verificación:  

La hoja de verificación se utiliza para reunir datos basados en la observación del comportamiento de un proceso con el fin de detectar tendencias, por medio de la captura, análisis y control de información relativa al proceso. Básicamente es un formato que facilita que una persona pueda tomar datos en una forma ordenada y de acuerdo al estándar requerido en el análisis que se esté realizando. Las hojas de verificación también conocidas como de comprobación o de chequeo organizan los datos de manera que puedan usarse con facilidad más adelante.

 

  3.   Lista de verificación

La lista de verificación, como su nombre lo dice, es la enumeración de una serie de pasos o requisitos a cumplir para realizar un determinado proceso, como si fuera una lista que se hace antes del supermercado para evitar olvidar algo.

Pero además de enumerar, esta herramienta también lleva una secuencia lógica en los requisitos, de tal forma que nos ayuda a recorrer el camino en menos tiempo.La memoria es una excelente ayuda para todos, pero es una realidad que bajo presiones de tiempo y estrés, podemos olvidar cosas sencillas o aun de sentido común. En estos casos, una lista de verificación es un apoyo ideal para recordar lo importante.

 

4.   Diagrama de dispersión:    

También llamado gráfico de dispersión, es un tipo de diagrama matemático que utiliza las coordenadas cartesianas para mostrar los valores de dos variables para un conjunto de datos. Los datos se muestran como un conjunto de puntos, cada uno con el valor de una variable que determina la posición en el eje horizontal y el valor de la otra variable determinado por la posición en el eje vertical.

 

5.   Gráfico de control: 

Es una representación gráfica de los distintos valores que toma una característica correspondiente a un proceso. Permite observar la evolución de este proceso en el tiempo y compararlo con unos límites de variación fijados de antemano que se usan como base para la toma de decisiones.

 

6.   Histograma: 

Es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables, normalmente señalando las marcas de clase, es decir, la mitad del intervalo en el que están agrupados los datos.  Los histogramas son más frecuentes en ciencias sociales, humanas y económicas que en ciencias naturales y exactas. Y permite la comparación de los resultados de un proceso.

 

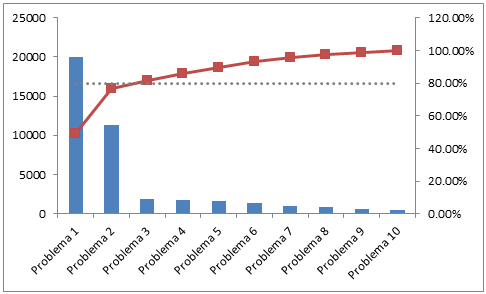
 7.   Diagrama de pareto:

También llamado curva 80-20 o distribución C-A-B, es una gráfica para organizar datos de forma que estos queden en orden descendente, de izquierda a derecha y separados por barras. Permite asignar un orden de prioridades. El diagrama permite mostrar gráficamente el principio de Pareto (pocos vitales, muchos triviales), es decir, que hay muchos problemas sin importancia frente a unos pocos graves. Mediante la gráfica colocamos los “pocos vitales” a la izquierda y los “muchos triviales” a la derecha.

Unidad 3 Planes de muestreo.

Del desarrollo tanto de los conceptos como de los ejemplos se puede observar el enorme potencial que posee la utilización del Control Estadístico de la calidad como instrumento y herramienta destinada a un mejor control en la evolución de la empresa, una forma más eficaz de tomar decisiones en cuanto a ajustes, un método muy eficiente de fijar metas y un excepcional medio de verificar el comportamiento del sistema.

Muchos son los que por desconocimiento de la forma en que funcionan los procesos tienden a efectuar prolongados y obstinados análisis en la búsqueda de las razones que dieron lugar a la variación de los costos en relación a los estándares o a los registrados en el período anterior, cometiendo el error de adoptar medidas de ajuste, cuando en realidad las variaciones respondían a la naturaleza misma del proceso, por lo que los ajustes dan origen a mayores diferencias en el futuro.

                 Muestreo simple doble múltiple de la calidad.

El plan de muestreo doble es la extensión natural del plan de muestreo simple. Se toma una muestra de n1 unidades y se observan las unidades defectuosas. Si el número de defectuosos no excede el número de aceptación c1 se acepta el lote. Si en cambio excede c1 pero no excede c2 se toma una segunda muestra de tamaño n2 y se contabilizan los defectos acumulados de la primera y segunda muestra. Si este acumulado de unidades defectuosas no excede c2 se acepta el lote y en caso contrario se rechaza. Notar que si el número de unidades defectuosas de la primera muestra es mayor a c2 no es necesario tomar una segunda muestra y el lote se rechaza inmediatamente. El siguiente diagrama resume el procedimiento descrito:

Ejemplo de Muestreo Doble

Consideremos un lote de tamaño de N=1.000 unidades sobre el cual queremos realizar un muestreo doble que tiene las siguientes características:(n1,c1)=(50,2) y (n2,c2)=(10,4). El porcentaje histórico de unidades defectuosas en lotes de similares características ha sido de un p=2%. Se desea estimar la probabilidad de aceptación del lote.

Un paso usual para abordar esta clase de procedimientos es desarrollar undiagrama que muestre las distintas combinaciones que permiten aceptar un lote luego de ser expuesto al plan de muestreo. En este caso en particular el diagrama es el siguiente:

Por ejemplo, si en la primera muestra se encuentran 3 unidades defectuosas se aplica una segunda muestra de tamaño 10, donde se aceptará el lote si la cantidad de unidades defectuosas en esta muestra es 0 o 1 (con esto se tiene un acumulado de defectuosos en ambas muestras menor o igual a c2=4).

Para estimar la probabilidad de aceptación del lote en el caso de la primera muestra se utiliza la Distribución de Poisson.En el caso de la segunda muestra se utiliza la Distribución Binominal.Las condiciones que permiten seleccionar dichas distribuciones se describen en la sección de muestreo simple.

En resumen la Probabilidad de Aceptación del Lote queda definido por la siguiente expresión donde Pp se refiere a una probabilidad obtenida a través de la Distribución de Poisson y Pb una probabilidad obtenida con la Distribución Binominal:

PA = Pp(0) + Pp(1) + Pp(2) + Pp(3)*[Pb(0) + Pb(1)] + Pp(4)*Pb(0)

Las  probabilidades se pueden calcular fácilmente haciendo uso de una planilla de cálculo. La siguiente imagen muestra las fórmulas utilizadas. Notar que ambos casos el argumento "Falso" en la fórmula indica que sólo se requiere estimar la probabilidad puntual y no acumulada.

En consecuencia la probabilidad de aceptación del lote es:

PA = 0,3679 + 0,3679 + 0,1839 + 0,0613*[0,8171 + 0,1667] + 0,0153*0,8171 = 99,25%

Se concluye que la probabilidad de aceptación del lote es de un 99,25%. Las probabilidades puntuales calculadas anteriormente se pueden obtener adicionalmente a través de tablas de probabilidad las cuales usualmente se encuentran disponibles en la bibliografía asociada a la Gestión de Calidad.